Recurso Educativo Digital de Matemáticas
“La aventura del conocimiento”
Realizado por Oscar Mena
⭐ El Valor Posicional en el Sistema de Numeración Decimal

✨ ¡Bienvenidos al mundo de los números! ✨
En este recurso educativo digital vamos a viajar juntos por diferentes ideas matemáticas que usan las personas en todo el planeta.
Aprenderás cómo cada número tiene un lugar importante, cómo leerlos y escribirlos, y cómo representarlos en la recta numérica.
También descubrirás que sumar y restar no solo sirven para resolver problemas en clase… ¡sino que han sido herramientas para el comercio, la agricultura y la vida cotidiana desde hace miles de años!
En cada actividad podrás jugar, pensar, resolver retos y trabajar con tus compañeros.
📚 Tu misión: entender que las matemáticas están en todas partes… y que muchas culturas han ayudado a construirlas.
🔢 ¡Prepárate para comenzar! ¿Listo para descubrir que los números cuentan historias?
⭐ Antes de empezar

✨ Recordemos la multiplicación de los numeros naturales ✖️
Cuando tienes que sumar varios valores iguales, se resuelven con una multiplicación.
🎮 Juega con la multiplicacion de una cifra 🎮 Juega con la multiplicacion de dos cifras 🎮 Juega con ejercicios de multiplicacion✨ Recordemos la división de los numeros naturales ➗
Cuando tienes que repartir o dividir en partes iguales, se resuelven con una división.
🎮 Juega con la división de una cifra 🎮 Juega con la división de dos cifras 🎮 Juega con ejercicios de división📄 ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen⭐ El valor de la posición en los números naturales

Puedes ver este video para que tengas una idea
El Sistema de Numeración Decimal es el que usamos todos los días para escribir números. Se llama decimal porque está formado por 10 dígitos:
0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
Pero… ¿cómo podemos escribir números tan grandes usando solo estos diez dígitos?
👉 Gracias al valor posicional.
🎯 ¿Qué es el valor posicional?
Es el valor que tiene un número según el lugar (posición) donde está escrito.
No vale lo mismo un 5 en:
- 5
- 50
- 500
Aunque es el mismo dígito, su valor cambia porque su posición es diferente.
📍 Las posiciones son importantes
De derecha a izquierda:
| Posición | Nombre | Significa que el número vale… |
|---|---|---|
| 4 | Unidad | Vale lo mismo: 4 = 4 |
| 40 | Decena | Vale 10 veces más: 4 = 40 |
| 400 | Centena | Vale 100 veces más: 4 = 400 |
| 4000 | Unidad de mil | Vale 1.000 veces más: 4 = 4.000 |
🔎 Ejemplo fácil
Observemos el número:
3482
Descomponemos según sus posiciones:
- 3 → está en las unidades de mil → vale 3.000
- 4 → está en las centenas → vale 400
- 8 → está en las decenas → vale 80
- 2 → está en las unidades → vale 2
Entonces:
3.482 = 3.000 + 400 + 80 + 2
🎮 Juega con el valor posicional🎉 Otra forma divertida de entenderlo: ¡el ábaco!
Imagina que tienes un ábaco, una herramienta antigua que sirve para contar y hacer operaciones.
Cada columna del ábaco representa un valor posicional:
- La primera columna es la de unidades.
- La segunda columna es la de decenas.
- La tercera columna es la de centenas.
- La cuarta columna es la de unidades de mil.
- La quinta columna es la de decenas de mil.
- La sexta columna es la de centenas de mil.
- La séptima columna es la de unidades de millón.
- Y así sucesivamente.
📄 ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen📘 Lectura y escritura de números de hasta 9 cifras
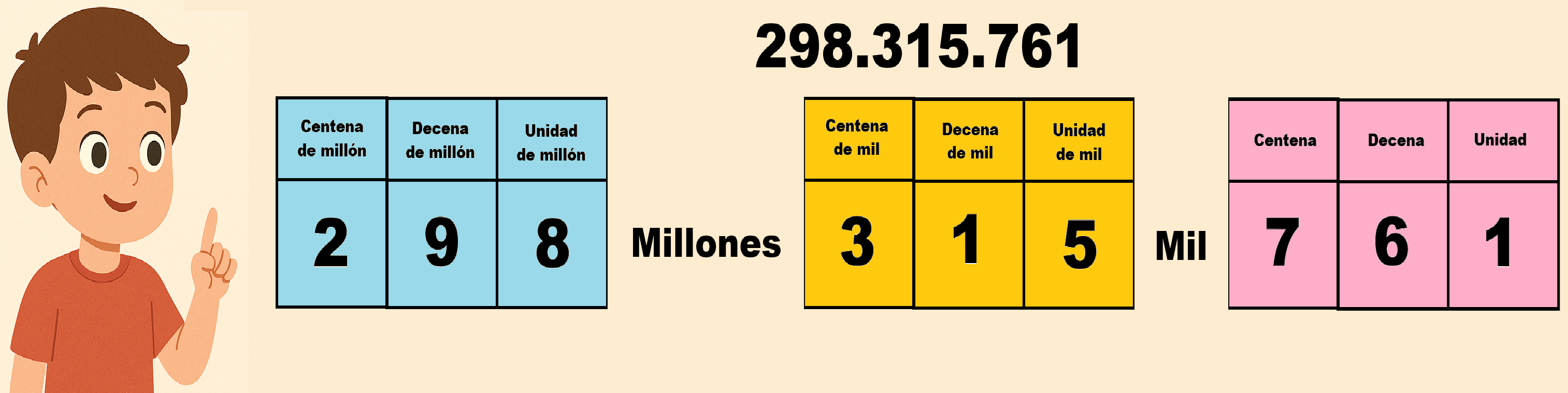
🧠 Antes de empezar:
Un número grande se lee por grupos de tres cifras, de derecha a izquierda:
👉 Unidad — Mil — Millón
Cada grupo de tres se llama período.
🧮 Los períodos del sistema decimal (hasta 9 cifras)
| Período | Columnas dentro del período | Ejemplo |
|---|---|---|
| Unidades | unidades – decenas – centenas | 345 → trescientos cuarenta y cinco |
| Miles | unidades de mil – decenas de mil – centenas de mil | 678 000 → seiscientos setenta y ocho mil |
| Millones | unidades de millón – decenas de millón – centenas de millón | 901 000 000 → novecientos un millones |
🧩 Ejemplo con un número completo
Número: 324 857 916
Vamos a leerlo por períodos:
📦 Período de millones
324 → trescientos veinticuatro millones
📦 Período de miles
857 → ochocientos cincuenta y siete mil
📦 Período de unidades
916 → novecientos dieciséis
👉 Lectura completa:
➡️ trescientos veinticuatro millones ochocientos cincuenta y siete mil novecientos dieciséis
🎮 Juega con la lectura de números✍️ ¿Cómo escribir números con palabras?
Regla sencilla:
➡️ Empieza por millones → luego miles → luego unidades.
➡️ Lee cada grupo como si fuera un número aparte.
📌 No uses “y” entre millones/miles/unidades, solo dentro del grupo según las reglas del español:
- 245 → doscientos cuarenta y cinco
- 804 → ochocientos cuatro (sin “y”)
🤓 Tip súper importante
Los ceros NO se leen cuando están solos en un período.
Ejemplo:
- 300 000 020 → trescientos millones veinte
- No decimos “cero mil”.
📄 ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen🧠 Ubicación de los números en la recta numérica
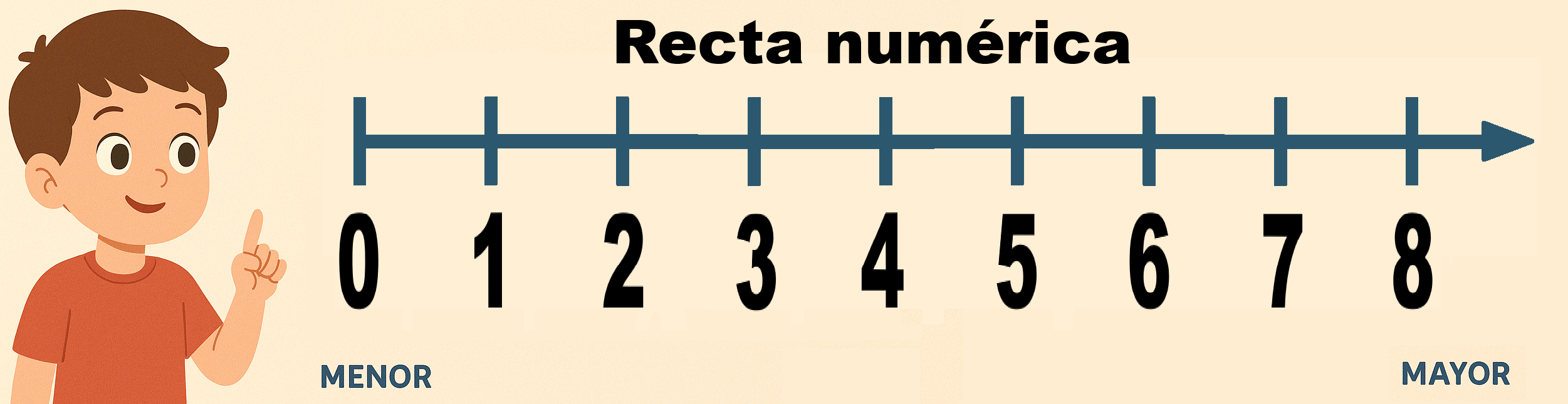
La recta numérica es una línea donde los números se colocan de izquierda a derecha.
👉 Cada número tiene un lugar fijo.
🌟 Ideas clave para enseñar a niños de primaria
1. La recta va de menor a mayor
- A la izquierda están los números más pequeños.
- A la derecha están los números más grandes.
➡️ 0 — 1 — 2 — 3 — 4 — 5 — 6 — …
2. La distancia entre números es siempre igual
No importa el número:
La distancia entre 2 y 3 es igual a la distancia entre 50 y 51.
3. Podemos ubicar números grandes o pequeños
No solo van enteros pequeños.
También podemos marcar números como 200, 500 o 1.000.
🧩 Ejemplos
🔹 Ubicar el número 7
- Buscamos el 0
- Contamos hacia la derecha
- Paramos en el 7
🔹 Ubicar el 34
- Sabemos que está entre 30 y 40
- Marcamos un punto un poco después del 33 → 34
🧠 Ubicar números con saltos
Se puede usar la recta para sumar, restar, multiplicar y dividir.
➕ Sumar
Si a 4 le sumas 3:
- Empiezas en 4
- Saltas 3 espacios a la derecha
- Llegas a 7
Haz clic en la siguiente imagen:
🎮 Juega con la suma en la recta numérica➖ Restar
Si a 9 le restas 4:
- Empiezas en 9
- Saltas 4 espacios a la izquierda
- Llegas a 5
Haz clic en la siguiente imagen:
🎮 Juega con la resta en la recta numérica✖️ Multiplicar
Si a 2 le multiplicas 4:
- Empiezas en 0
- Haces 4 saltos de 2 espacios a la derecha
- Llegas a 8
Haz clic en la siguiente imagen:
🎮 Juega con la multiplicación en la recta numérica➗ Dividir
Si divides 10 entre 3:
- Empiezas en 10
- Cuentas los saltos que puedas hacer de 3 espacios hacia la izquierda
- No puedes pasarte del cero
- Si llegas al cero, el resto o residuo es cero
- Si no llegas al cero, donde llegaste es el resto o residuo
Haz clic en la siguiente imagen:
🎮 Juega con la división en la recta numérica📄 ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen🧠 Las propiedades y relación entre la adición (suma) y la sustracción (resta)

🌟 1. ¿Qué es la adición?
Es juntar o agregar cosas.
👉 Ejemplo:
Si tienes 4 caramelos y te dan 3 más:
4 + 3 = 7
➕ La suma aumenta
Cada vez que sumas, el número crece.
🎮 Juega con ejercicios de la suma🌟 2. ¿Qué es la sustracción?
Es quitar o separar cosas.
👉 Ejemplo:
Si tienes 7 caramelos y regalas 3:
7 − 3 = 4
➖ La resta disminuye
Cada vez que restas, el número baja.
🎮 Juega con ejercicios de la resta🧩 3. La adición y la sustracción son operaciones inversas
👉 La resta “deshace” la suma.
👉 La suma “deshace” la resta.
📌 Ejemplos:
- Si 5 + 2 = 7, entonces 7 − 2 = 5
- Si 10 − 6 = 4, entonces 4 + 6 = 10
🔁 Van juntas como un par de amigos.
🧠 4. Propiedades importantes de la suma
📌 A. Propiedad conmutativa
No importa el orden de los sumandos:
3 + 4 = 4 + 3
📌 B. Propiedad asociativa
Podemos agrupar sin cambiar el resultado:
(2 + 3) + 4 = 2 + (3 + 4)
📌 C. Elemento neutro
Sumar 0 no cambia el número:
8 + 0 = 8
👉 🧠 En la resta, estas propiedades no funcionan igual
(no es lo mismo 10 − 3 que 3 − 10).
🎯 5. Cómo usar su relación en problemas
📦 Si conoces una suma, puedes encontrar una resta.
Ejemplo:
- “Tengo 12 galletas, me comí 5. ¿Cuántas quedan?”
➡️ Primero: 12 − 5 = 7
➡️ Luego puedes comprobar: 7 + 5 = 12
📄 6. ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen🟠 Números racionales

📌 ¿Qué son los números racionales?
👉 Son números que se pueden escribir como una fracción, es decir:
Número racional =
📗 El número de arriba se llama numerador.
📘 El número de abajo se llama denominador.
👉 El denominador no puede ser 0.
🍕 Ejemplos con cosas del día a día
- Si partes una pizza en 4 y comes una parte:
- Si tomas media chocolatina:
- Si compartes una naranja en 3:
1/4 → un cuarto de pizza.
1/2 → la mitad.
1/3 → una tercera parte.
💡 También pueden ser decimales
Los números racionales no solo son fracciones:
- 0,5 es lo mismo que 1/2
- 0,25 es lo mismo que 1/4
- 2,75 es lo mismo que 2 + 3/4
📌 Si un decimal se puede convertir a fracción → es racional.
🧠 Regla fácil de recordar
🔴 Todo número que puedas decir “algo dividido entre algo” es racional.
Ejemplos:
- 3 = 3/1
- 5/2
- 0,1 = 1/10
- 7/4
📏 En la recta numérica
Los números racionales están entre los enteros.
👉 Entre el 0 y el 1 hay muchos:
1/2, 1/3, 3/4, 0,25, 0,75…
👉 Entre el 2 y el 3 también:
2,5 → 2 1/2
2,25 → 2 1/4
2,75 → 2 3/4
📣 ¡La recta numérica está llena de números racionales!
🔵 Vamos a comparar fraccionarios en la siguiente imagen:
🔵 Vamos a ubicar números en la recta numérica:
🎮 Juega practicando con las fracciones📄 6. ¡Veamos cuánto has aprendido!
✍️ Realiza el siguiente examen🔢 Operaciones combinadas

✨ ¿Qué son las operaciones combinadas?
Son ejercicios donde aparecen varias operaciones juntas: sumas, restas, multiplicaciones, divisiones y paréntesis.
👉 El truco está en hacerlas en el orden correcto.
🧠 🌟 La regla mágica: P M D A S
📌 Primero Paréntesis
📌 Luego Multiplicación y División (de izquierda a derecha)
📌 Después Adición (suma) y Sustracción (resta) (también de izquierda a derecha)
💡 Esto se llama orden de operaciones.
🟡 Ejemplo muy sencillo
👉 3 + 2 × 4
1. Primero multiplicación: 2 × 4 = 8
2. Luego suma: 3 + 8 = 11
📣 ¡El resultado es 11!
⚠️ ❗ No se hace 3 + 2 = 5 primero, porque la multiplicación va antes.
🔵 Ejemplo con paréntesis
👉 (5 + 3) × 2
1. Primero el paréntesis: 5 + 3 = 8
2. Luego multiplicación: 8 × 2 = 16
🟢 Ejemplo un poco más largo
👉 10 − 4 × 2 + 3
1. Multiplicación: 4 × 2 = 8
2. Operamos de izquierda a derecha:
10 − 8 = 2
2 + 3 = 5
➡️ Resultado: 5
🙌 Truco para recordar
🎩 “Paréntesis manda”
⭐ Después vienen las operaciones fuertes → multiplicar y dividir
🙂 Y al final las suaves → sumar y restar